Salve, salve, galerinha! Essa postagem é bem especial para nós do Explicaê. Isso porque esse assunto delicioso é o que mais caiu no ENEM em todos esses anos. Trata-se da Razão e da sua fiel escudeira, a Proporção!
Só aluno Explicaê Premium tem acesso as provas e gabaritos de vestibulares de todo o Brasil.

Matematicamente falando, a razão é um sinônimo de fração, ou seja, uma divisão! Certo?
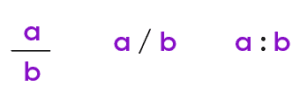
E a proporção? A proporção é simplesmente uma igualdade entre duas ou mais razões.

Mas vamos falar um pouquinho mais sobre as razões? Existem algumas razões bem interessantes para a gente estudar! Uma delas é a velocidade média.

NÃO! A velocidade é uma razão, e quem estuda as razões é a Matemática, ora bolas! A Física apenas pega emprestado hahahaha 😊
A velocidade média é a razão entre a distância percorrida e o tempo gasto. Porém, podemos pensar de uma maneira mais ampla sobre o conceito de velocidade.
Inclusive usamos a palavra velocidade para se referir a outras grandezas que não têm nada a ver com distância.
Por exemplo, podemos pensar na velocidade com que uma pessoa consegue ler as páginas de um livro, ou a velocidade com que um computador consegue baixar as maravilhosas apostilas autorais do Explicaê, ou ainda a velocidade de um ar condicionado, ou por fim a velocidade com que a água jorra de uma torneira ou mangueira. Essa última velocidade, inclusive, é bem famosa e recebe o nome de vazão.
Só aluno Explicaê Premium tem correções ilimitadas das suas redações.
Ora, são inúmeras as aplicações de velocidade e apenas uma delas tem a ver com distância percorrida! Pode chorar e se espernear à vontade, Física!

Bom, após acalmar a galera da Física, vamos continuar?!
Outra razão que vale a pena a gente estudar é a densidade. Calma, calma, calma …

A densidade também é uma razão, e quem estuda as razões? A Matemática! 😊
A densidade é a razão entre a massa de um corpo e o seu volume. Entretanto, há outras maneiras de imaginar uma densidade.
Podemos pensar, por exemplo, na densidade de uma folha de papel que nem aquela questão que caiu na 1ª aplicação do ENEM 2020. Nesse caso, estávamos mais interessados na relação entre a massa do papel e sua superfície, ou seja, tínhamos uma densidade superficial.
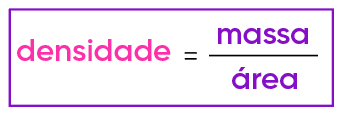
Seguindo uma ideia muito parecida, podemos pensar na densidade linear de uma corda ou de um fio, por exemplo, em que estamos interessados na relação da massa com o seu comprimento.

Além disso tudo, ainda podemos pensar em uma densidade populacional que se trata da razão entre o número de indivíduos e a área. Ou seja, aquela famosa aglomeração!

Em tempos de pandemia até dói na alma ver uma imagem dessas, não é verdade? Então, nada de aglomerar, ou seja, nada de ficar em um local com uma grande razão entre o número de pessoas e a área!

Vamos em frente com as nossas razões especiais? E agora abram alas para a mais importante razão para o ENEM: a escala! E antes que o pessoal da Geografia fale alguma coisa, escala não tem necessariamente a ver com mapas! Podemos falar de escala envolvendo mapas, desenhos, fotos, maquetes, miniaturas, entre outros.
A escala é a razão entre o comprimento de algo em um mapa, desenho, foto, maquete, miniatura, entre outros, e o seu comprimento real. Vamos usar a expressão comprimento virtual para representar esse comprimento no mapa, desenho, foto, maquete, miniatura, entre outros. Assim:

Certa vez eu fui para Nova York e, como todo bom turista, comprei uma miniatura da Estátua da Liberdade. É claro que a curiosidade me dominou e, assim que cheguei no hotel, a primeira coisa que fiz foi medir a altura da Estátua em miniatura, obtendo 31 cm. Rapidamente entrei na internet e procurei qual era sua altura real e vi que era 93 m.

Como fazer agora para encontrar a escala? Ora é só dividir a altura da miniatura pela altura real. Porém, cuidado!!! Temos que ter as duas medidas na mesma unidade. Assim, a altura real de 93 m, precisei transformar para centímetros, ou seja, 93 x 100 = 9300 cm.
Continuando a minha saga, eu dividi as duas alturas e obtive:
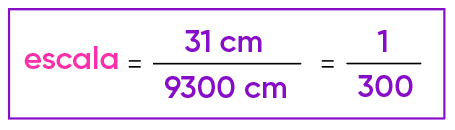
Assim, a escala que obtive foi 1 : 300, a mesma que tinha escrito na caixa da miniatura. Resumindo, tive um trabalhão para nada! ☹
Ahh, não esquece, a escala é adimensional, ou seja, não tem unidade!
Só aluno Explicaê Premium tem acesso a dúvidas ilimitadas.
Bem, continuando a falar sobre escalas, existem algumas situações em que há a necessidade de comparar áreas ao invés de comprimentos, por exemplo, em uma foto.

A pergunta é: podemos relacionar a escala com áreas? Podemos sim! Porém, devemos ter um cuidado a mais.
Como a área é uma grandeza com duas dimensões (comprimento e largura), dizer por exemplo que a escala de uma foto é 1 : 10, é o mesmo que dizer que o comprimento real é 10 vezes maior e que a largura real é 10 vezes maior também que o comprimento e largura da foto. Ou seja, a área real será 10 x 10 = 102 = 100 vezes maior que a área da foto!
Assim, quando formos comparar a área real com a área da foto, devemos lembrar de elevar a escala ao expoente 2. Assim:

Por fim, existem alguns problemas que envolvem relações entre volumes. Por exemplo, podemos citar novamente a miniatura da Estátua da Liberdade ou a maquete de um shopping que irá ser inaugurado.
Podemos relacionar a escala com volume? Novamente a resposta é sim! 😊 Mas há, mais uma vez, um cuidado que devemos tomar.
Como o volume é uma grandeza com três dimensões (comprimento, largura e altura), dizer que a escala de uma miniatura é 1 : 300 é o mesmo que dizer que o comprimento real é 300 vezes maior, a largura real é 300 vezes maior e que a altura real é 300 vezes maior que o comprimento, largura e altura da miniatura. Ou seja, o volume real será 300 x 300 x 300 = 3003 = 27.000.000 vezes maior que o volume da miniatura!

E aí não teve jeito! Peguei minha miniatura da Estátua da Liberdade é mergulhei em um copo cilíndrico com líquido, calculei a altura que o líquido subiu, multipliquei por πr2 e obtive 200 cm3. Como a escala é 1 : 300, o volume real da Estátua da Liberdade é 200 x 3003 = 5.400.000.000 cm3 =5.400 m3.
Procurei na internet para saber o volume da Estátua e não encontrei essa informação! Ainda bem que eu sou um bom matemático. O que seria de mim se não soubesse o volume desse monumento tão famoso no mundo!!!
Só aluno Explicaê Premium tem correções ilimitadas das suas redações.

