Salve, salve, galerinha! Quando estudamos as funções quadráticas, um dos tópicos que mais aparecem em vestibulares, bem como no ENEM, são os chamados problemas de valores máximos e mínimos da função do 2º grau.
Sabemos que o gráfico de uma função quadrática tem a forma de uma parábola e que, a depender do valor do coeficiente de x2, essa parábola pode ter a concavidade voltada para cima ou para baixo. Portanto, podemos distinguir dois casos:
Só aluno Explicaê Premium tem acesso ilimitado a mais de 6.000 livros em PDF.
1º caso) O coeficiente de x2 é positivo (a > 0)
Nesse caso, a parábola terá a concavidade voltada para cima e a função terá um valor mínimo.

Isso significa dizer que todos os valores que a função assume serão maiores ou iguais a esse valor mínimo.
2º caso) O coeficiente de x2 é negativo (a < 0)
Nesse caso, a parábola terá a concavidade voltada para baixo e a função terá um valor máximo.

Isso significa dizer que todos os valores que a função assume serão maiores ou iguais a esse valor mínimo.
E lá vai a dica do tio Rígel para não esquecer mais nunca!

Passada a sessão piadas nerds, vamos voltar ao que interessa!
É importante perceber que, nos dois casos, o valor mínimo e o valor máximo são iguais ao y do vértice (YV).
Rígel, isso significa dizer que os valores máximo e mínimo são iguais? NÃO! Isso significa dizer que os valores máximo e mínimo são calculados da mesma maneira. Quando a parábola estiver para cima (carinha feliz), o valor é mínimo e, quando a parábola estiver para baixo (carinha triste), o valor é máximo.
Devemos lembrar também a fórmula para calcular o y do vértice (YV), bem como o x do vértice (XV). São elas:

Agora vamos ao que interessa: como os vestibulares e o ENEM podem perguntar sobre valores máximos e mínimos? Bem, temos algumas situações possíveis:
A primeira situação, e a mais fácil, é quando a função quadrática já é fornecida no enunciado da questão. Por exemplo, vamos supor que um canhão lançou um projétil e a altura h, em metros, desse projétil é dada pela função h(t) = – 2t2 + 18t + 9, em que t representa o tempo, em segundo, desde o lançamento. O gráfico dessa função é:

Observe que a função atinge seu valor máximo (parábola para baixo) no ponto V que é o vértice da parábola. Nessa primeira situação, podem ser feitas duas perguntas: qual o valor máximo da função, que no caso será a altura máxima que o projétil atinge ou para que valor de t a função atinge seu valor máximo?
Caso a questão peça o valor máximo da função, o que está sendo pedido é o y do vértice (YV). Caso a questão peça o instante em que essa função atinge seu valor máximo, o que está sendo pedido é o x do vértice (XV). Vamos calcular cada um desses valores?
O x do vértice será:

Para o y do vértice, vamos calcular antes o valor do delta:

Assim, o y do vértice será:

Agora vamos interpretar esses valores? Vem com o tio Rígel!
O YV representa o valor máximo da função, isso significa dizer que o projétil do canhão subiu a altura máxima de 49,5 metros para depois cair até o solo.

Por outro lado, o XV representa o tempo que se passou, desde o disparo do canhão, que o projétil levou para atingir essa altura máxima. Assim, o projétil demorou 4,5 segundos desde quando ele foi disparado para atingir essa altura máxima.
Incrível, não é mesmo?
Bom, mas agora vamos dificultar as coisas, até porque aqui é o blog do Explicaê e não temos espaço para amadores!!! E se a questão não fornecer a função?
Nessa segunda situação, o mais comum dos contextos é o problema da promoção!

Para que serve uma promoção? O vendedor baixa o preço de um produto com o objetivo de vender mais, correto? Mas até que ponto é viável baixar o preço? Se o vendedor baixar muito o preço, vai vender mais, mas pode correr o risco de vender muito barato e não ter uma grande receita.
Vamos ver um exemplo na prática? Tem uma pizzaria aqui do lado do condomínio em que eu moro. Todos os dias eu passo por ela e tem uma faixa escrita assim:

Daí um desses dias eu parei e comprei uma pizza portuguesa, na verdade eu comprei duas para comer a outra no dia seguinte! Pizza dormida é a melhor coisa do mundo!!!
Enfim, comprei a pizza e sugeri ao dono da pizzaria que mudasse a promoção para PIZZA GRANDE por APENAS R$ 39,00. Ia “perder” R$ 1,00, mas com certeza iria vender muito mais!
Em outro dia, estava caminhando com meu gatinho Gauss e o dono da pizzaria me chamou e disse: – Rapaz, não é que deu certo o que você sugeriu? Antes eu vendia 10 pizzas por dia por R$ 40 cada; quando coloquei o preço por R$ 39 passei a vender 12 pizzas por dia!
Você nesse instante deve estar pensando: Nossa, que diferença enorme, foi quase a mesma coisa!
Na verdade, não! Vendendo 10 pizzas por R$ 40, temos uma receita de 10 x 40 = R$ 400 por dia, já vendendo 12 pizzas por R$ 39, temos uma receita de 12 x 39 = R$ 468 por dia. Isso nos dá um aumento de R$ 68 na receita, ou seja 17% a mais. Isso tudo com apenas uma redução de R$ 1,00 no valor da pizza! 😊
Ahhh, antes que eu esqueça, a receita que eu estou falando não é a receita da pizza não! Chamamos de receita, que também pode ser chamada de arrecadação ou faturamento, o total obtido com as vendas. Nesse caso específico da pizza, a receita será a multiplicação da quantidade de pizzas vendidas pelo preço unitário da pizza.

Agora vamos à pergunta: se a cada redução de R$ 1 no preço da pizza, a quantidade de pizzas vendidas aumentasse em 2 unidades, qual será o preço que tornará a receita máxima?
Vamos pensar um pouco! A tabela a seguir ilustraria algumas possibilidades de preço, quantidade vendida e receita.
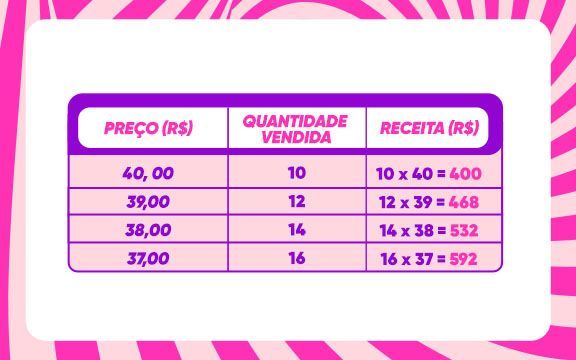
Observe que a receita vai aumentando, conforme o preço da pizza vai diminuindo. Mas isso vai acontecer para sempre? Claro que não! Se o dono da pizzaria continuar diminuindo o preço da pizza, vai ter um momento que a pizza vai estar tão barata que, mesmo vendendo uma quantidade grande, a receita obtida com as vendas será menor.
Então vamos repetir a pergunta: qual o preço ideal dessa pizza, ou seja, o preço que faz com que a receita seja máxima? Para isso, vamos tentar generalizar a situação:
Com base no preço da pizza por R$ 40 em que são vendidas 10 pizzas por dia, vamos supor que o dono da pizzaria dê x descontos de R$ 1, ou seja, cobre pela pizza R$ (40 – x). Tudo claro até aqui? Se ele der x descontos de R$ 1, isso significa um desconto único de x reais em relação ao preço inicial que era R$ 40. Por isso o preço após esses descontos será R$ (40 – x).
Por outro lado, a cada desconto de R$ 1, são vendidas 2 pizzas a mais. Assim, se forem dados x descontos de x reais, serão vendidas 2x pizzas a mais. Ok?
Assim, após os x descontos iremos vender (10 + 2x) pizzas a um preço de R$ (40 – x) cada pizza. Beleza, beleza?
Dessa forma, a receita R, em reais, será:

Nem pense em “simplificar” essa receita por 2, o dono da pizzaria vai ficar com muita raiva de você! Afinal, você dividirá o pobre dinheiro que ele vai receber por 2. Que pensamento feio você teve!
Pois bem! O gráfico dessa função da receita será:

Para descobrirmos o preço ideal, vamos primeiro encontrar o x do vértice da função.

Agora, cuidado! Esse valor de x não é o preço ideal. Apenas vamos usá-lo para encontrar esse preço. Lembra que o preço era R$ (40 – x) e eram vendidas (10 + 2x) pizzas? Pois bem:
O preço ideal será 40 – 17,5 = R$ 22,50 e, por esse valor, serão vendidas 10 + 2 . 17,5 = 10 + 35 = 45 pizzas por dia. A receita diária da pizzaria será 22,50 x 45 = R$ 1.012,50.
Nooooooooossa! A receita diária da pizzaria era de R$ 400 e passou para R$ 1.012,50, ou seja, um aumento de mais de 150% !!!!!!
O dono da pizzaria ficou muito, mas muito alegre comigo e foi assim que ele virou um concorrente da Pizza Hut.
Agora, todo dia que eu passo para levar Gauss para passear, ele ganha um pedaço de pizza! A Matemática não é mesmo uma linda (e deliciosa)?!


